Você conhece o Teorema de Bayes? Apesar de ser um conceito específico de probabilidade estatística, ele certamente está presente no seu cotidiano. Isso porque diversas áreas do conhecimento o utilizam em seus processos.
Além disso, entender o Teorema de Bayes traz vantagens para os profissionais que estão em busca de otimização de processos, pois ele é um recurso de funcionalidades múltiplas em diferentes ferramentas de análise.
Neste texto, a Frons vai explicar os principais pontos sobre esse teorema e de que forma ele pode ser aplicado. Confira a seguir e boa leitura!
Afinal, o que é o Teorema de Bayes?
Apesar de sistematizar uma teoria da probabilidade, Thomas Bayes acreditava na regularidade e previsibilidade do universo.
O Teorema de Bayes determina a probabilidade de um evento acontecer diante de um conhecimento prévio que pode estar relacionado a este evento.
Por isso, este teorema é uma fórmula matemática que utiliza a probabilidade condicional.
Isso significa que, na teoria da estatística e probabilidade, este teorema é uma forma de revisão das previsões diante de sólidas evidências.
Sendo assim, através de estimativas baseadas em um conjunto de indícios, é possível ter uma compreensão real daquele universo de dados.
Origem do teorema bayesiano
Mas como esse teorema surgiu?
Thomas Bayes foi um ministro protestante, que viveu na Inglaterra do século 18. Ele estudou na Escócia e se dedicou às suas duas grandes paixões: teologia e matemática.
Devido às suas contribuições na época, Bayes entrou em 1752 na Royal Society, instituição científica britânica. Apesar disso, ele viveu em relativa obscuridade.
Dois anos após a morte de Bayes, o seu amigo e filósofo Richard Price divulgou à Royal Society um artigo de autoria do reverendo. Nesse artigo, estava a demonstração do teorema matemático.
No entanto, quem desenvolveu o Teorema de Bayes foi o matemático francês Pierre-Simon Laplace. No século 19, Laplace formalizou o estudo de Bayes e mostrou como ele poderia ser aplicado.
O que é a inferência bayesiana
Assim como as ferramentas para mensurar qualidade, o Teorema de Bayes também possui diversas formas de ser aplicado.
Uma das formas de aplicar o Teorema de Bayes é por meio da inferência bayesiana.
Graças à inferência bayesiana, o teorema explica de que forma o grau de crença no acontecimento de um evento deve sofrer alteração, após considerar as evidências do fato deste acontecimento.
Com isso, o teorema de Bayes indica como alterar as probabilidades anteriores, diante de novas evidências, para conseguir probabilidades posteriormente. Em resumo: primeiro se aponta para a distribuição da probabilidade de parâmetros; depois, para a atualização após a observação dos elementos da amostra.
Fórmula do Teorema de Bayes
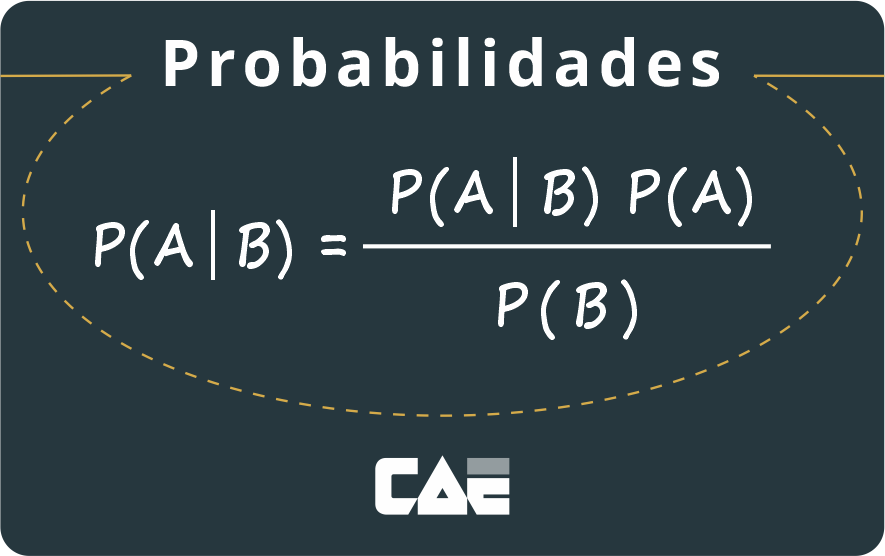
A representação matemática da fórmula do Teorema de Bayes é a seguinte:
Em que:
- A e B são eventos e P (B) é diferente de 0;
- P (A) e P (B) são as probabilidades a priori de A e B;
- P(B|A) é a probabilidade de B acontecer dado que A ocorreu;
- P(A) é a probabilidade de A ocorrer;
- P(B) é a probabilidade de B ocorrer.
Quer ter acesso a explicações mais detalhadas e acesso a novos conteúdos? Assine o canal do Youtube da Frons e confira conteúdos exclusivos.
Aplicação do Teorema de Bayes
Com relação à sua aplicação, o Teorema de Bayes emprega dois tipos de inferências: a intuitiva e a experimental. Primeiramente, a inferência intuitiva se fundamenta no conhecimento a priori de situações passadas. Uma possível probabilidade surge, sendo formulada a partir de uma análise da situação.
A inferência experimental, por sua vez, se relaciona com a experimentação dos dados. Ou seja, a partir deles são realizados procedimentos estatísticos para calcular a probabilidade. Com novos dados, os cálculos são refeitos e novas probabilidades surgem.
A Matemática e áreas afins, como a Estatística e a Probabilidade, a Engenharia, e a Computação, utilizam amplamente o Teorema de Bayes em suas pesquisas.
No entanto, outras áreas como a Medicina e de Ciências da Informação também utilizam este teorema para suas práticas.
Muitos profissionais da área de Tecnologia usam o Teorema de Bayes na construção de algoritmos, que indicam respostas mais apuradas.
Você sabia que muitas empresas utilizam esse teorema para melhorar suas práticas?
Um exemplo disso é a aplicação dele em ferramentas estatísticas que analisam os processos organizacionais.
Apesar de parecer distante da realidade dos colaboradores, esse tipo de investimento permite uma melhoria dos processos de gestão, como otimização do tempo.
Implementar novas técnicas é uma necessidade atual e precisa ser uma realidade da cultura organizacional das empresas modernas.
Bayes no problema de Monty Hall
Conhecido como Jogo das Portas, o problema de Monty Hall discute a mudança de probabilidades a partir de um certo grau de crença. Por exemplo, digamos que você está participando de um game show e tem três portas para escolher.
O prêmio está em apenas uma das portas. Você escolhe a porta número 1. O apresentador revela que a 3 está vazia e pergunta se você quer mudar para a porta número 2.
Então, é uma boa ideia mudar de porta?
A resposta é sim! E o Teorema de Bayes mostra como suas chances são duplicadas.
Em primeiro lugar, o grau de crença te faz considerar que o apresentador sabe onde está o prêmio.
Logo, escolher a porta número 1 (A) dá um terço de chances de ganhar. Ao eliminar a porta vazia número 3 (B), as chances se mantêm. Dessa forma, percebemos que P(A) = 1/3. Para calcular P(B), precisamos verificar as chances do apresentador abrir uma porta vazia.
Ou seja, quais são as probabilidades do apresentador abrir uma porta vazia, com você escolhendo ou não a porta certa?
Entendendo sobre probabilidades
As probabilidades são essas:
- P(A) = probabilidade do prêmio estar na porta número 1;
- P(B|A) = probabilidade do apresentador escolher a porta vazia, visto que o prêmio está na porta número 1;
- P(B|AC) = probabilidade do apresentador escolher uma porta vazia, visto que o prêmio NÃO está na porta número 1;
- P(AC) = probabilidade do prêmio NÃO estar na porta número 1.
Então, as chances do apresentador abrir uma das portas vazias, independente do prêmio estar ou não na porta escolhida, é igual a 1.
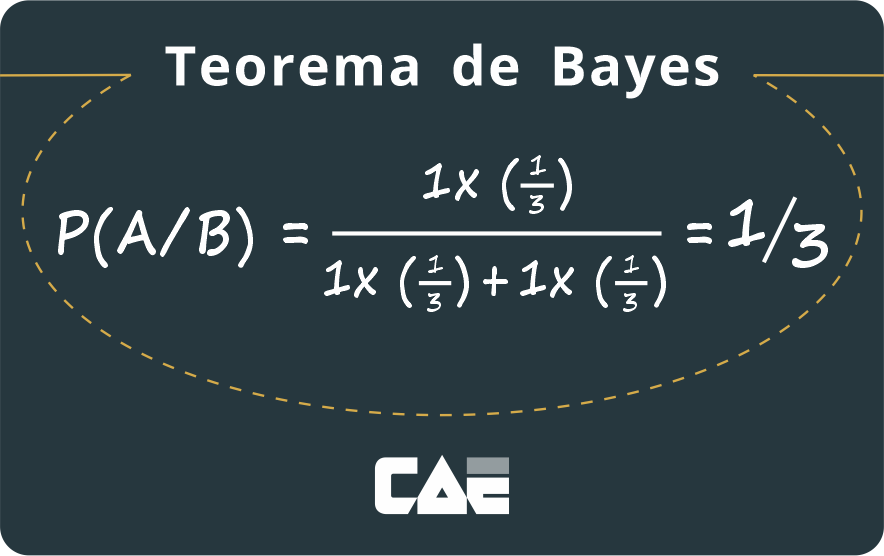
Sobre a chance da porta errada ser escolhida, a probabilidade é de dois terços. Portanto, se a primeira escolha for mantida a probabilidade de ganhar é:
Dessa forma, as chances ficam em 1/3. Se a troca for feita, porém, a probabilidade aumenta para 2/3.
Isso não garante que o prêmio seja ganho, mas aumenta suas chances.
Aprendeu a aplicabilidade do Teorema de Bayes? Conheça a Frons
Neste texto, elucidamos a importância e aplicabilidade do Teorema de Bayes. Por isso, agora te convidamos a conhecer a Frons.
Os cursos da Fronss oferecem formação completa em carreiras nas áreas de processos, operações, produção, qualidade, logística, entre outras.
Além disso, você terá um certificado de uma empresa que possui mais de 6 anos de expertise na área de cursos e treinamentos. Não perca essa oportunidade e se matricule!
E se tem interesse em aprofundar seus conhecimentos, acesse o Blog da Frons para ter acesso a mais conteúdo exclusivo.